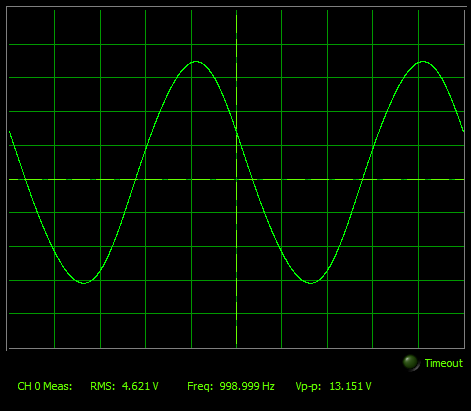
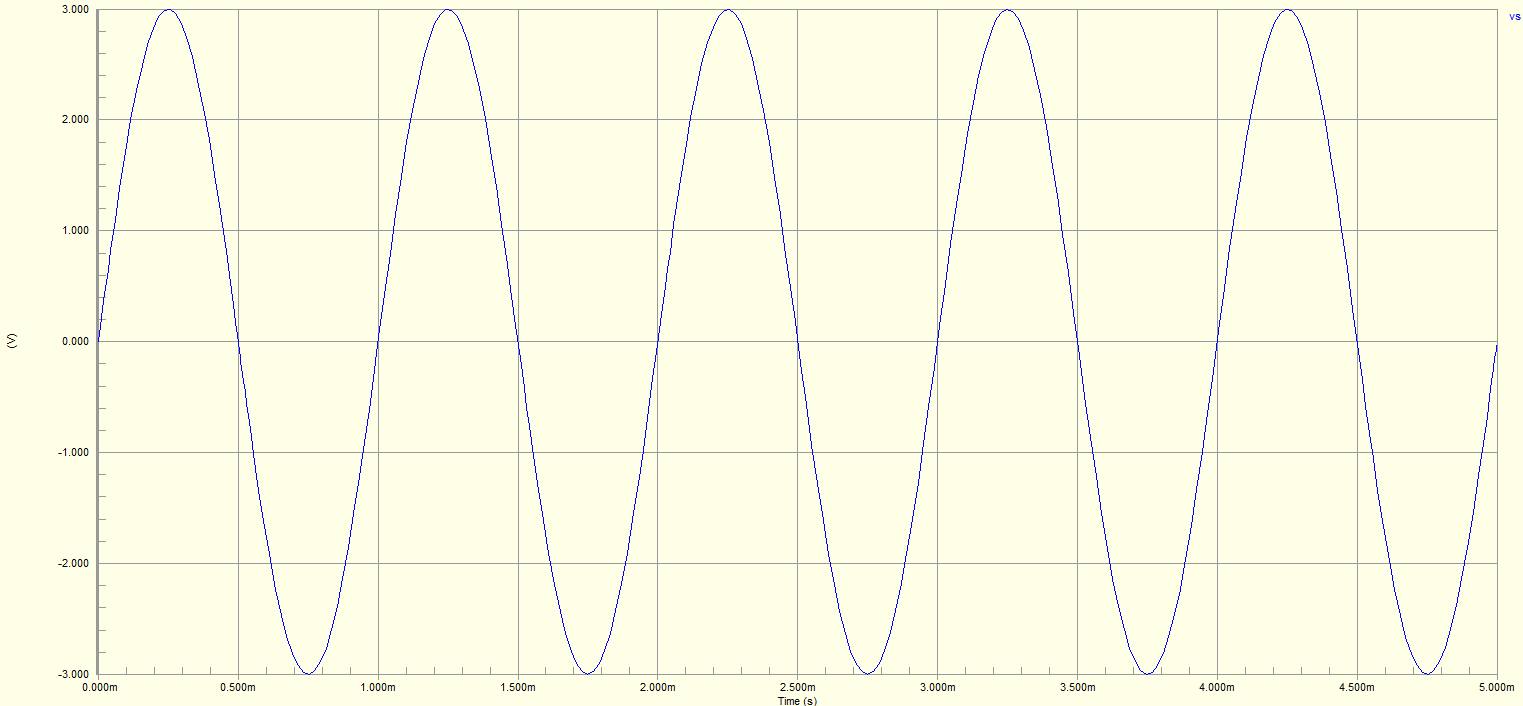
For starters, I made an op amp in an inverting configuration with a gain of 2. The op amp had rails of +/- 5 V, with an input of a 1 KHz sine wave, at 6 Volts peak to peak.
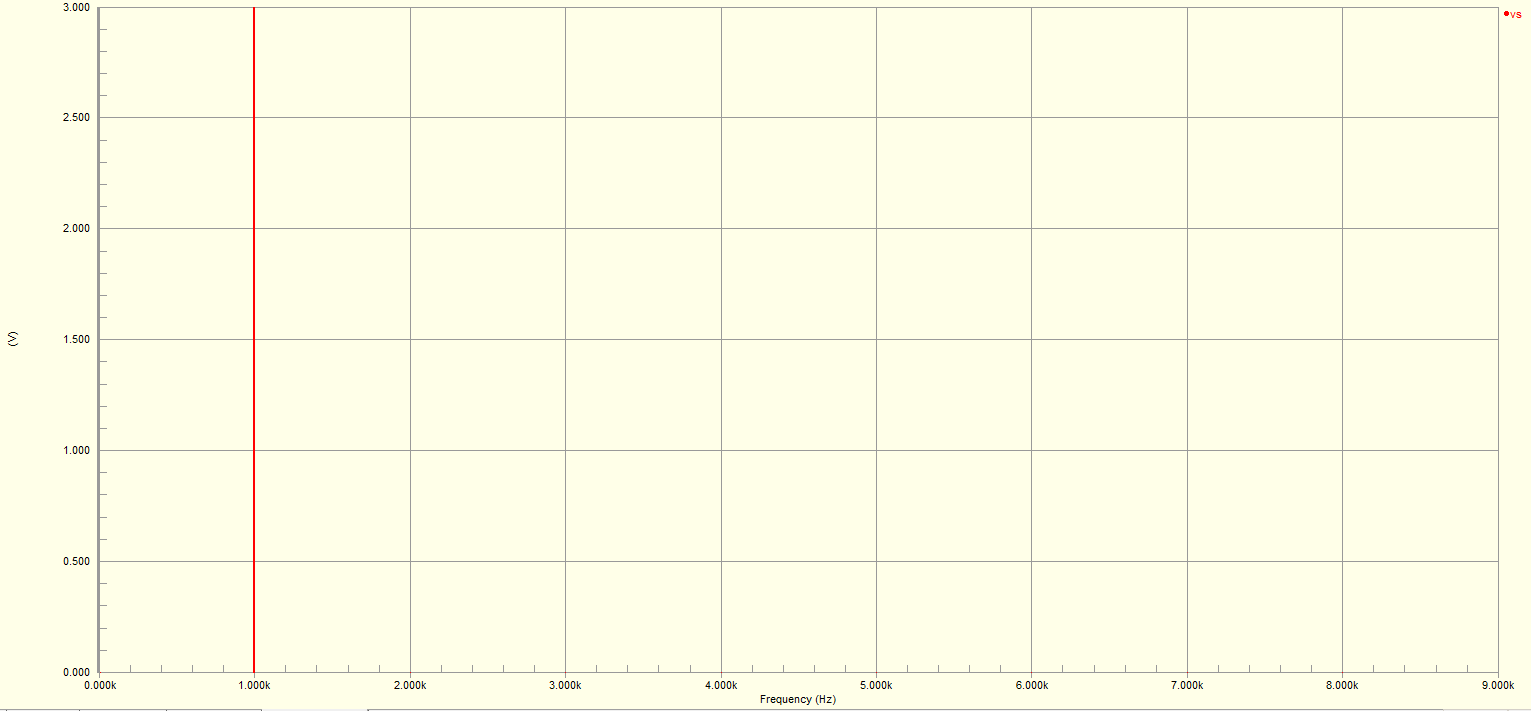
Taking a FFT of the input purely for comparison will give a single harmonic with an amplitude of 3V, at 1 KHz as expected.
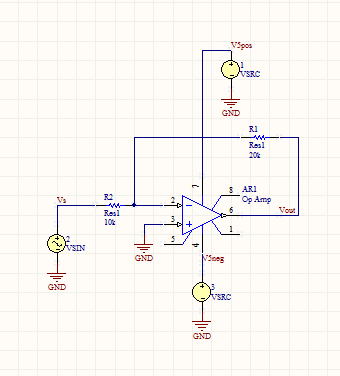
Based on the gain and the rails, along with the input signal, it is clear that there will be a good amount of clipping on the signal.
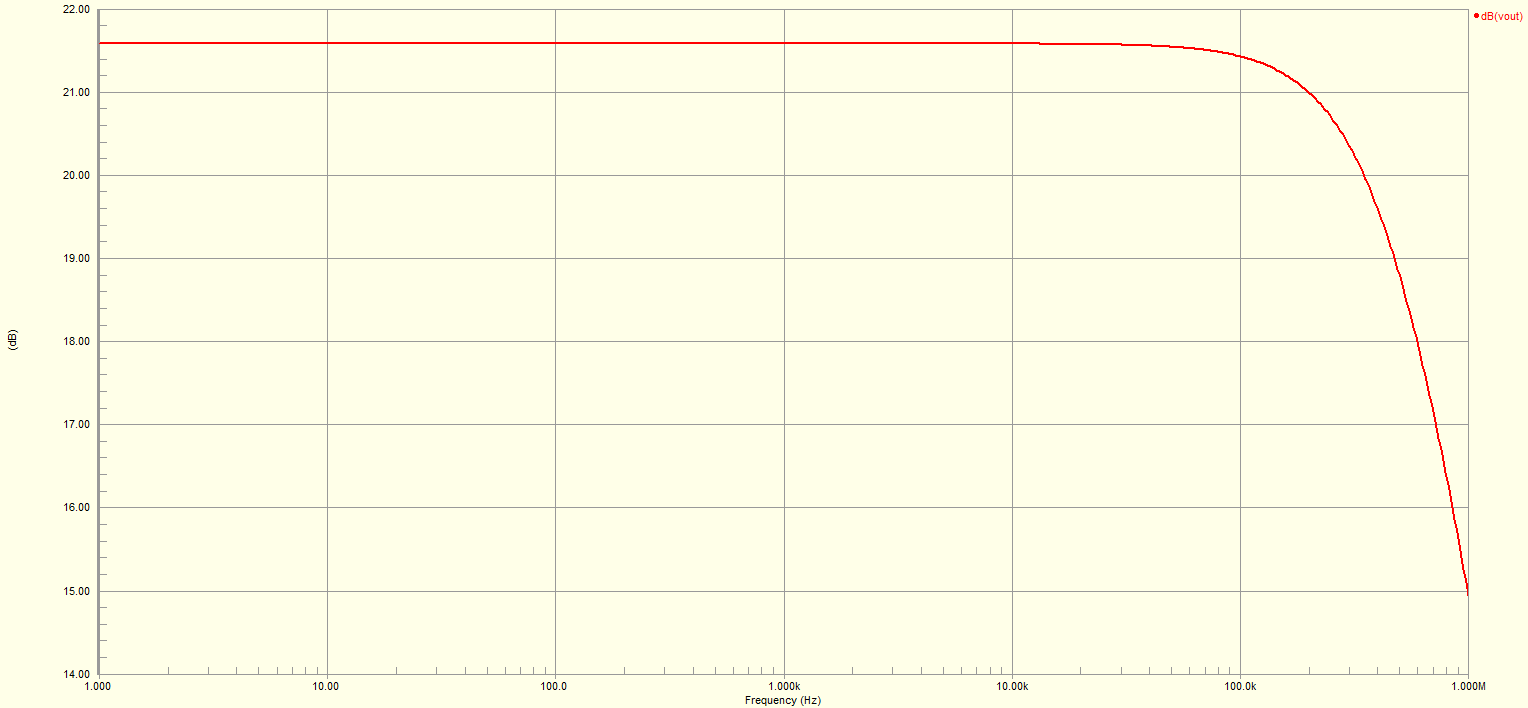
The above circuit gives the following Bode Plot:
After running the simulation the following output signal was observed:
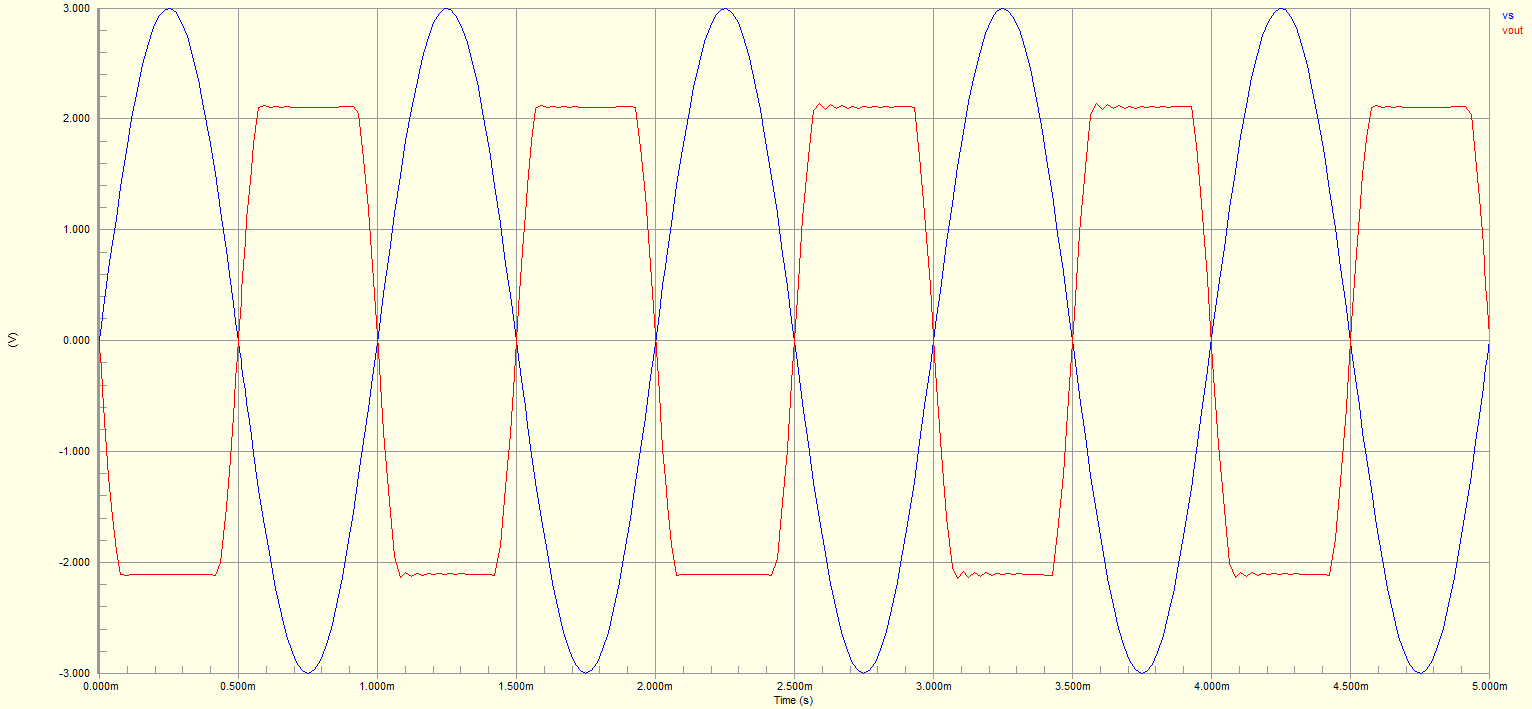
This output signal slightly resembles a square wave, which has a Trigonometric Fourier Transform of:
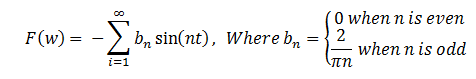
This can be easily observed from the nature of the function as there is no DC biasing (in simulation), eliminating any DC component and the function is odd, thus eliminating the cosine component. This produced the following FFT.
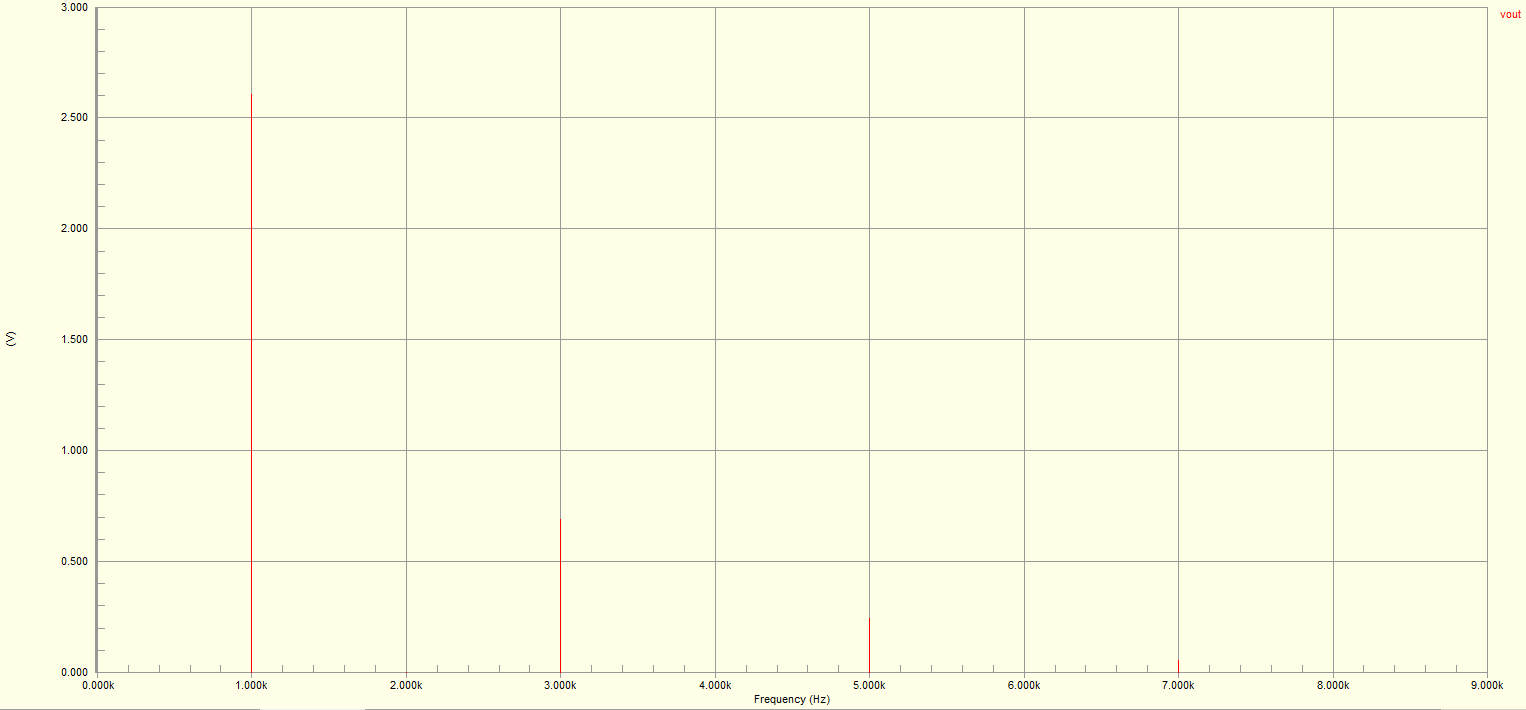
From Fourier analysis, the clipping has added additional harmonics outside of the fundamental frequency of 1KHz.
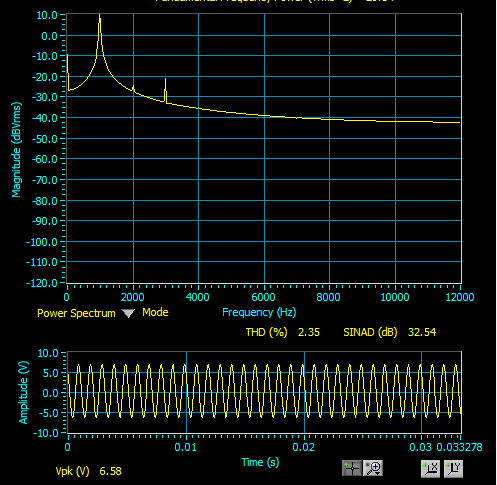
This was experimentally observed using an LM-324 Op-Amp.
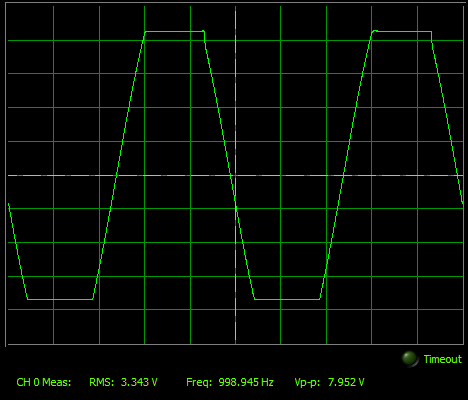
Due to the skew in the observed signal, the gradual changes in the signal prevent the zeroing out of the even harmonics, thus producing the below Fourier Representation.
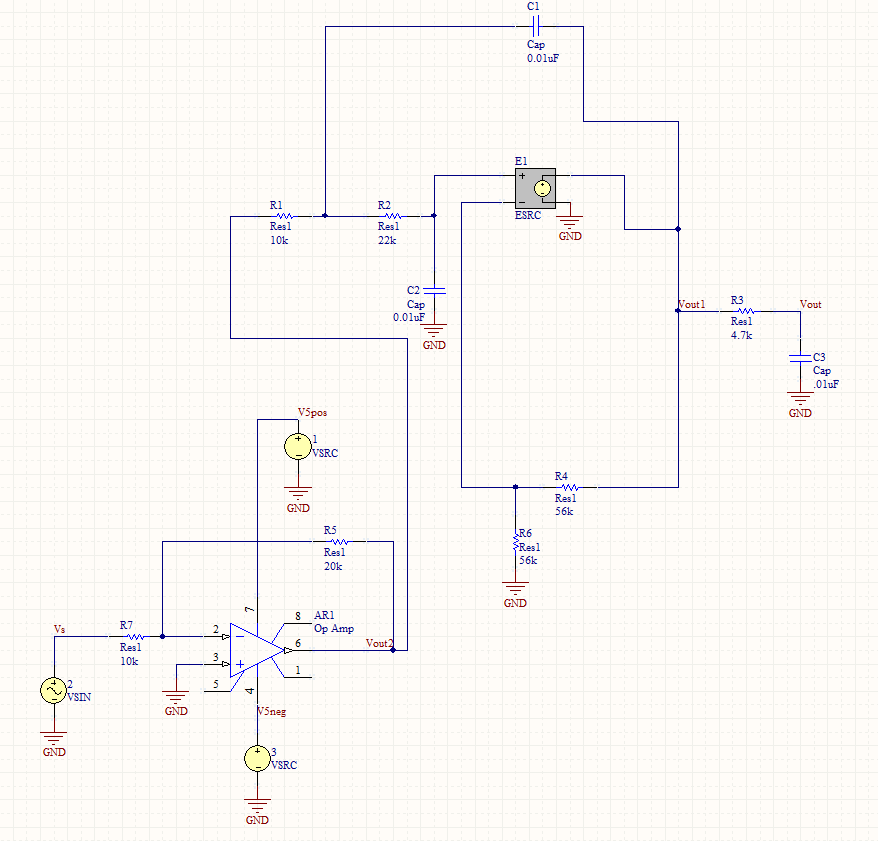
So what can be done about the clipping? Well, we need to attenuate the harmonics by a lot to get back to a clean signal, implying the need for a sharp filter (maybe a third order Low Pass Filter). Below is the schematic for a simple, active third order LPF which was connected to the clipping amplifier. Since the active filter will have +/- 15 V rails, it is safe to assume that there will be no clipping, thus I used an ideal voltage controlled voltage source (VCVS) to act as an Operational Amplifier.
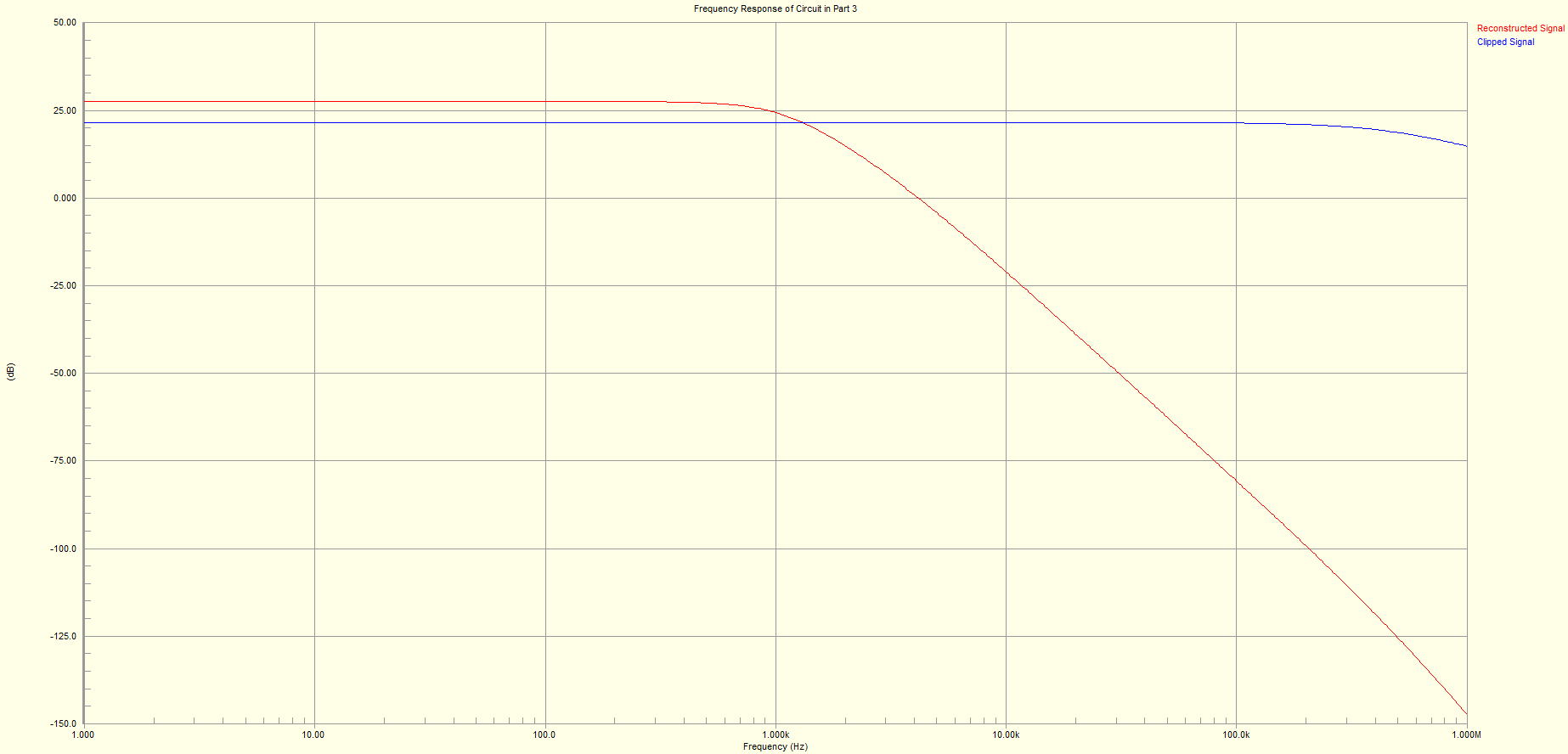
The filter has a break frequency of roughly 1KHz, as shown in the Frequency Analysis shown below. The Bode Plot also included the clipped signal, which is shown in blue.
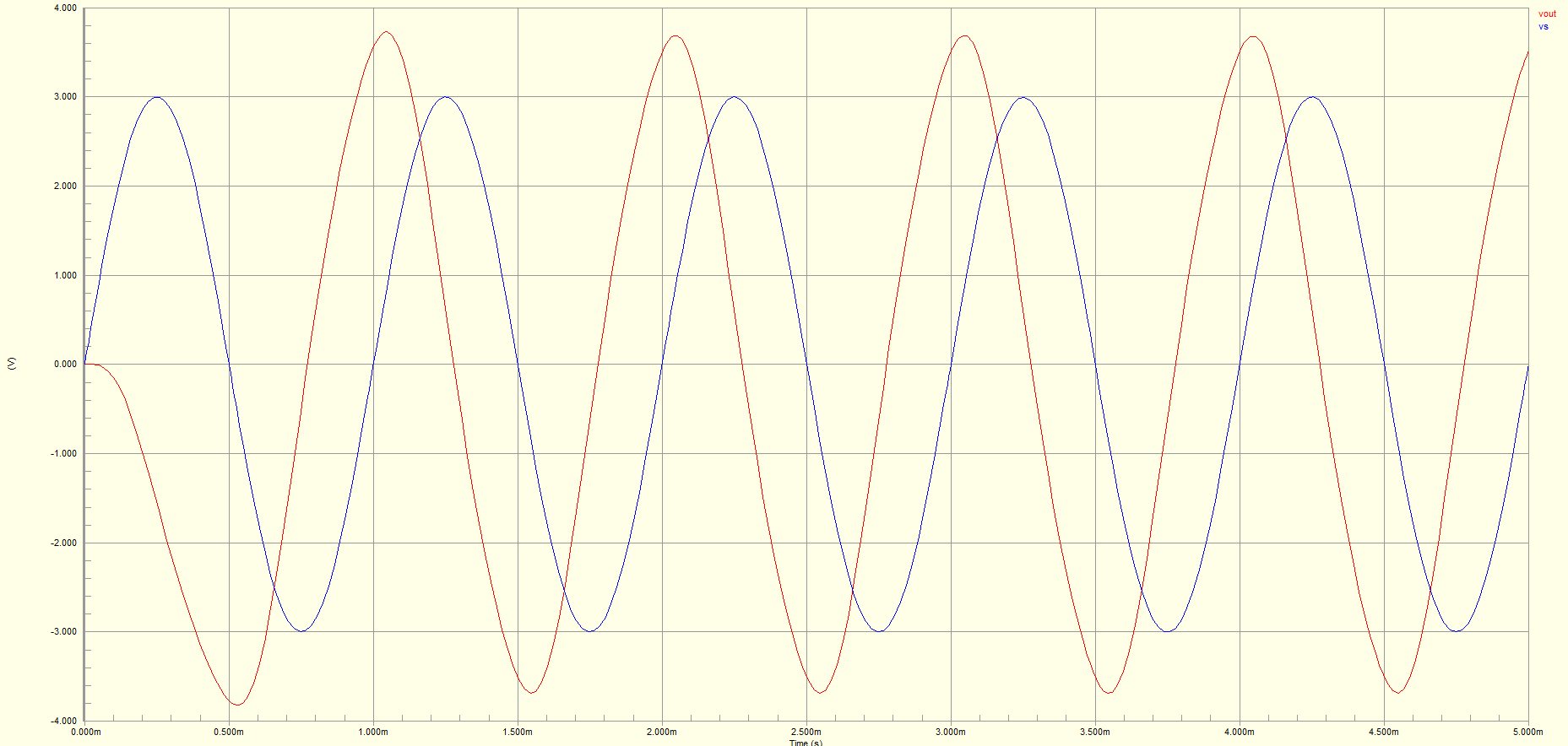
The Transient of the new circuit gives promising results, generating an output wave similar to that of a sine wave. The red line is the output of the third order LPF and the blue is the source signal applied to the circuit. Due to the nature of the filter, a 90 degree phase shift was observed.
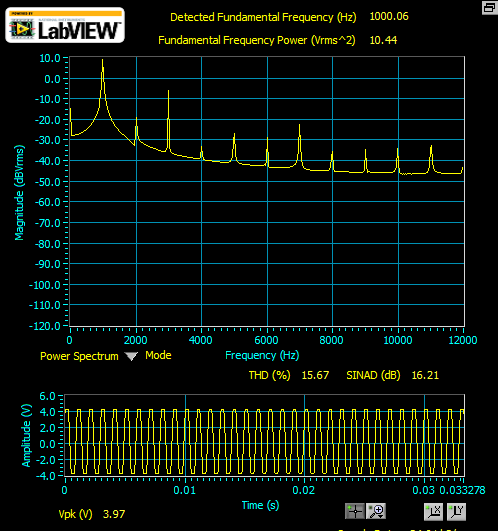
To see how close the output signal was to a perfect sine wave, a Fourier Analysis was run against the resulting signal producing:
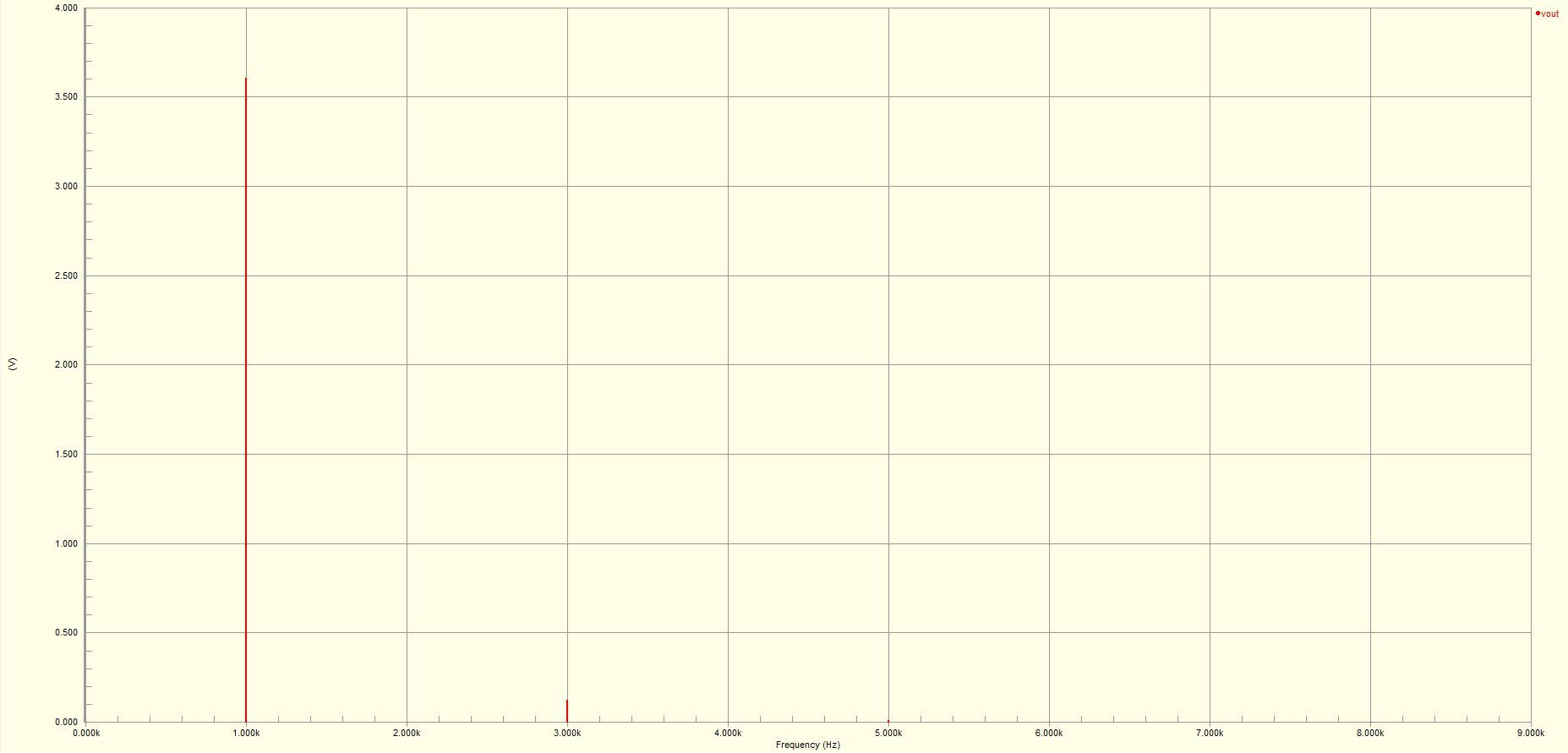
The resulting signal is extremely close with the only noticeable additional harmonic occurring at 3KHz.
The reconstruction filter was built and below is the resulting transients and frequency response.