Typical password security involves combining a salt with the password and then computing the hash. With a number of recent data breaches, storing passwords securely is increasingly important. Some major ones have been Yahoo! Voices, LinkedIn, and formspring. Yahoo! Voices was storing their passwords in plaintext, meaning no cracking was needed. LinkedIn used Secure Hash Algorithm 1 (SHA-1) without a salt. Finally, formspring used SHA-256 with a salt.
So even though the SHAs have been analyzed greatly by cryptographers, there are risks to using them. The SHA algorithms are extremely efficient, which is great news for the load on your server! However, it is just as good for an attacker, since computing the hash is the critical path when cracking.
This is where work factor algorithms such as bcrypt, a hashing implementation of the Blowfish Cipher come into play. A work factor algorithm allows compensation for Moore’s Law. As computing power increases, the work factor of the algorithm can increase accordingly. bcrypt is designed to also hog computer memory and have a logarithmic increase in resources required for each pass. Furthermore, bcrypt confines an attack on a hash to a single computer and cannot be effectively parallelized into GPU’s (Graphics Processing Unit).
A John the Ripper project was able to compute a single hash in 2,283,008 whereas a SHA-3 hash can be computed in a single clock cycle with 11 operations.
So to demonstrate, (and investigate) the scaling of hashing algorithms, I implemented a number of algorithms in Java, along with algorithms to act as baselines with a scaling constant so it would scale similar to bcrypt. The SHA algorithms scale as O(n)of the block size, typical of message digest based algorithms. Each test point was run 1,000 times and the average run time was used. Also, at each iteration, a random set of bytes was generated to prevent against any biasing.
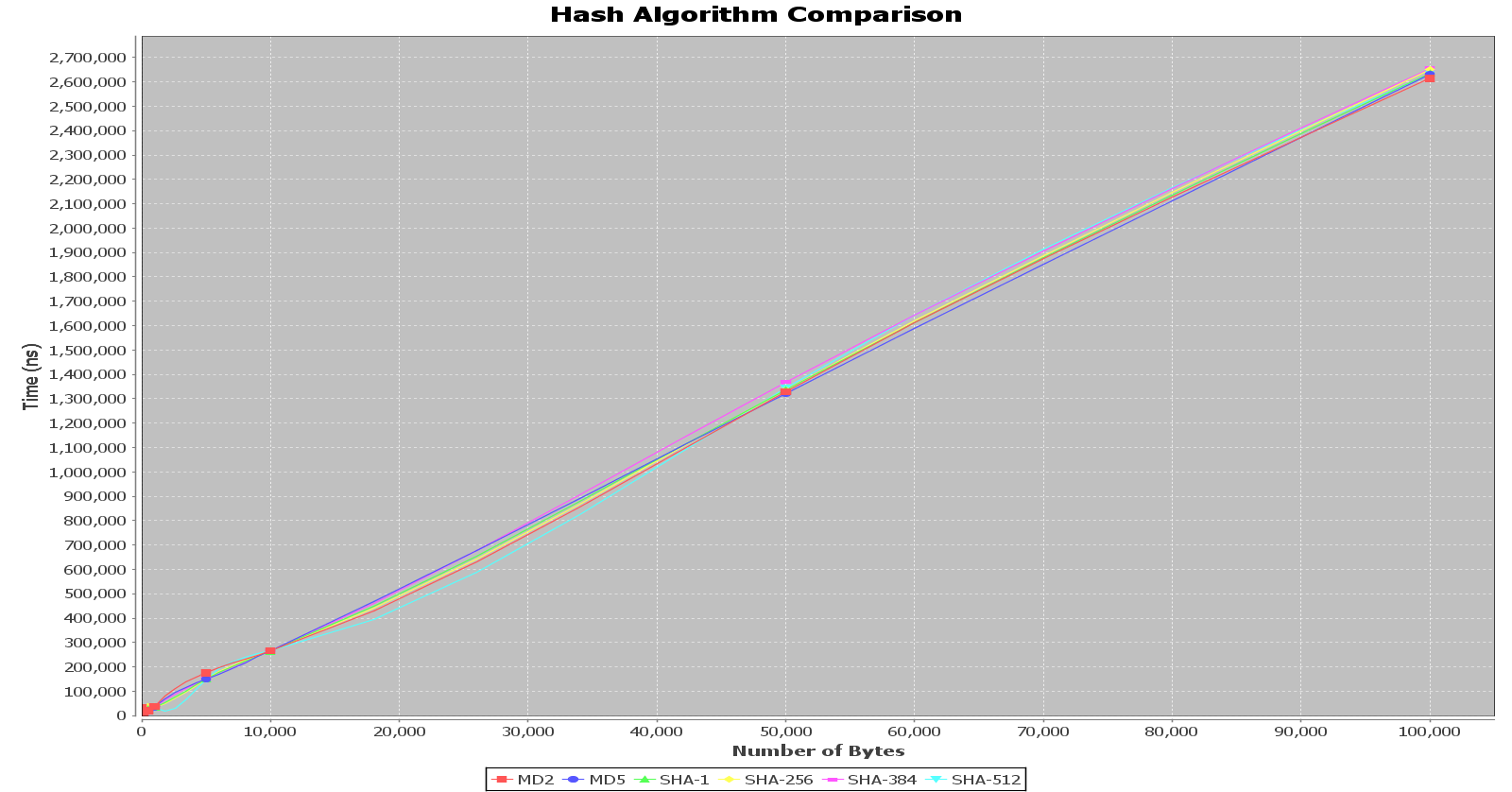
Once the scaling based on the message digest was understood, I standardized the byte length. bcrypt only operates on the first 72 characters and truncates the rest, so understanding the message length versus time complexity was not needed.
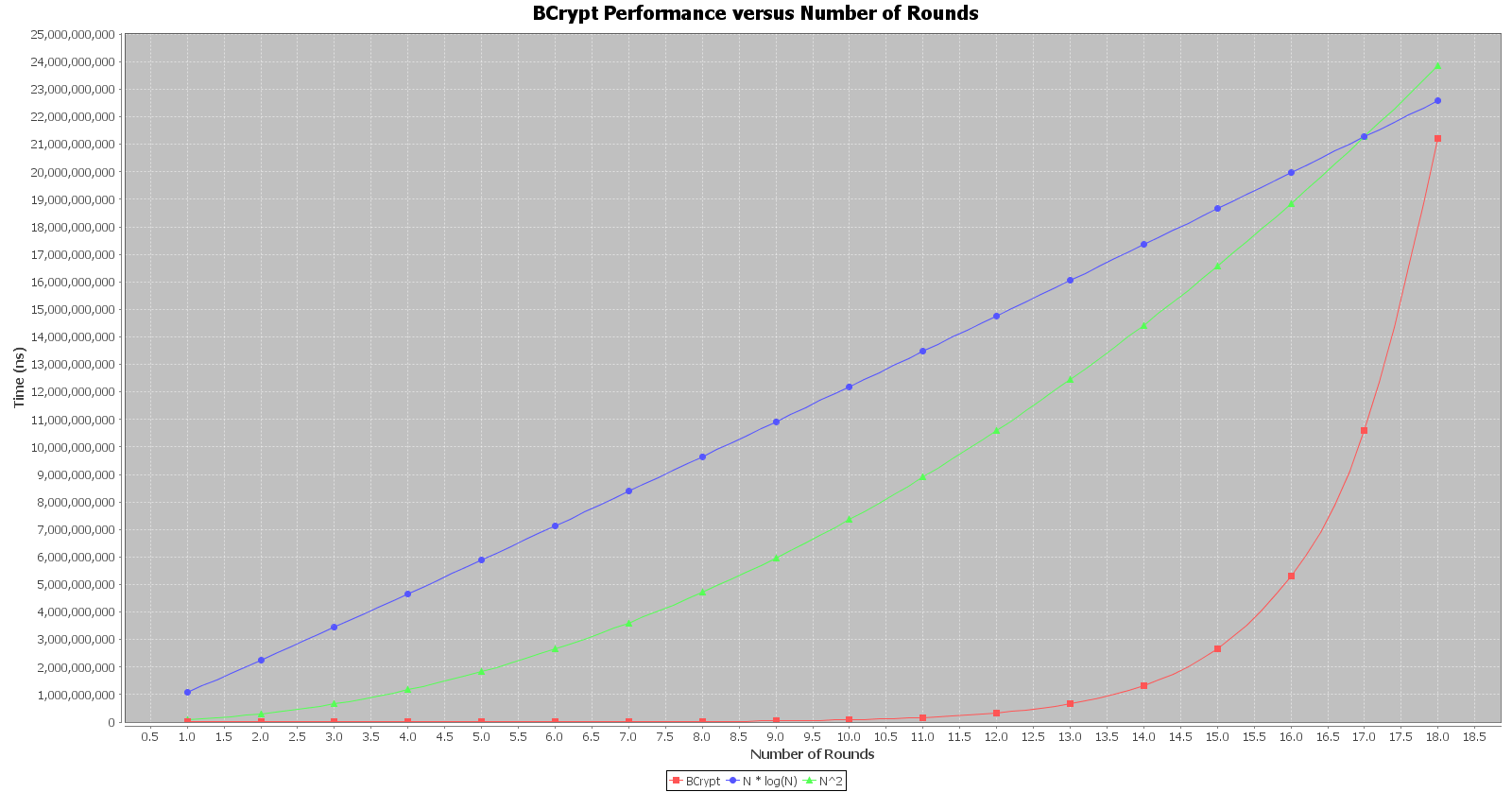
Since bcrypt is a work factor driven algorithm, I wrote a simple set of code to modify the work factor and determine how the algorithm scales. I also added in an ideal O(n log(n)) and O(n^2) that were scaled to fit the bcrypt curve better. I cut back the number of trials to 10 at each data point for bcrypt due to the time requirement.
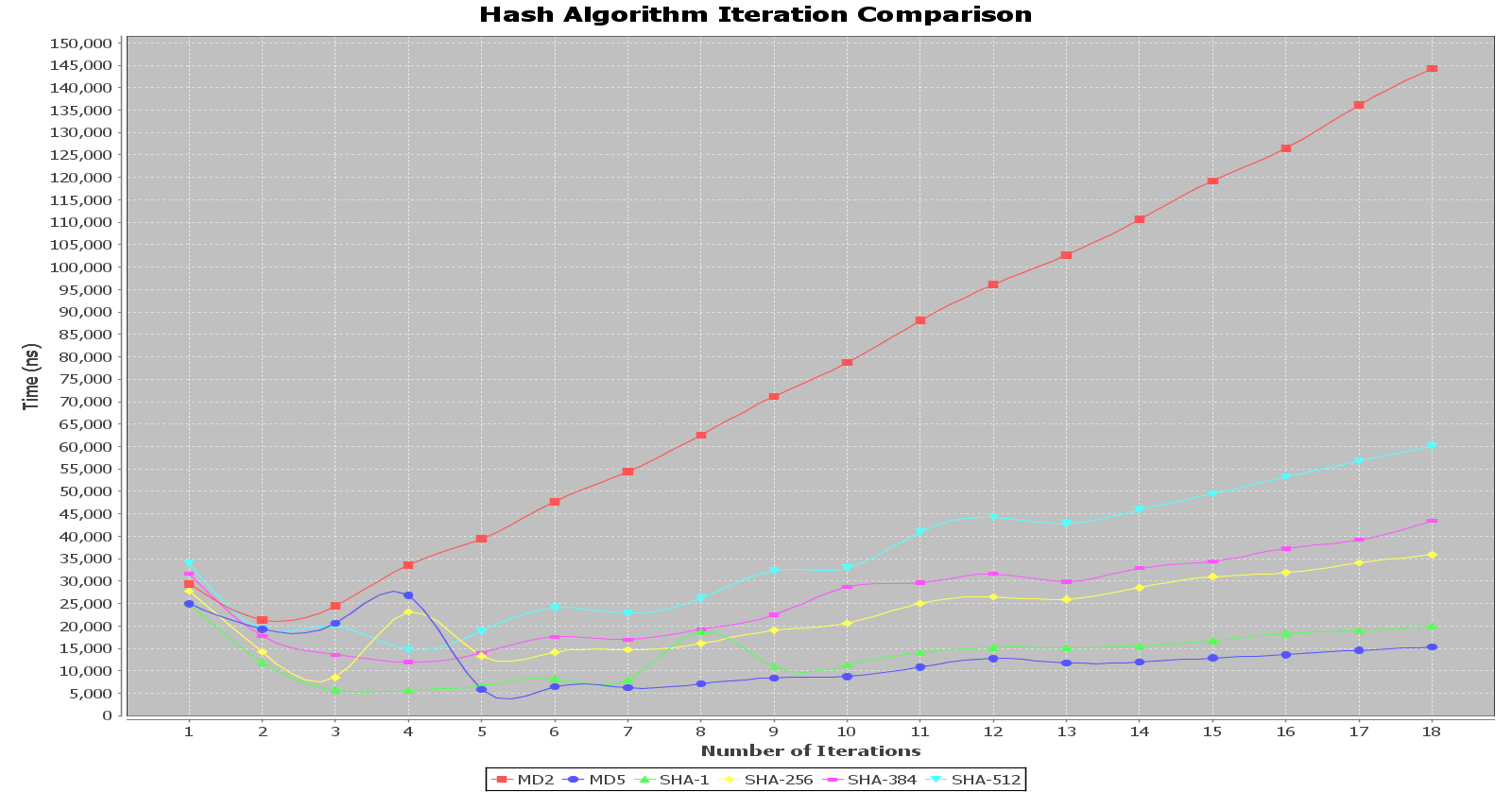
After looking at how bcrypt scales, I decided to look at the scaling of more common hashing algorithms under multiple iterations. I used 1,000 trials for each data point and averaged the results. I used a randomly generated 10 byte input into the hashing algorithms, and then continued rehashing the resulting hash for the number of iterations.
So how does SHA-512 rack up to bcrypt?
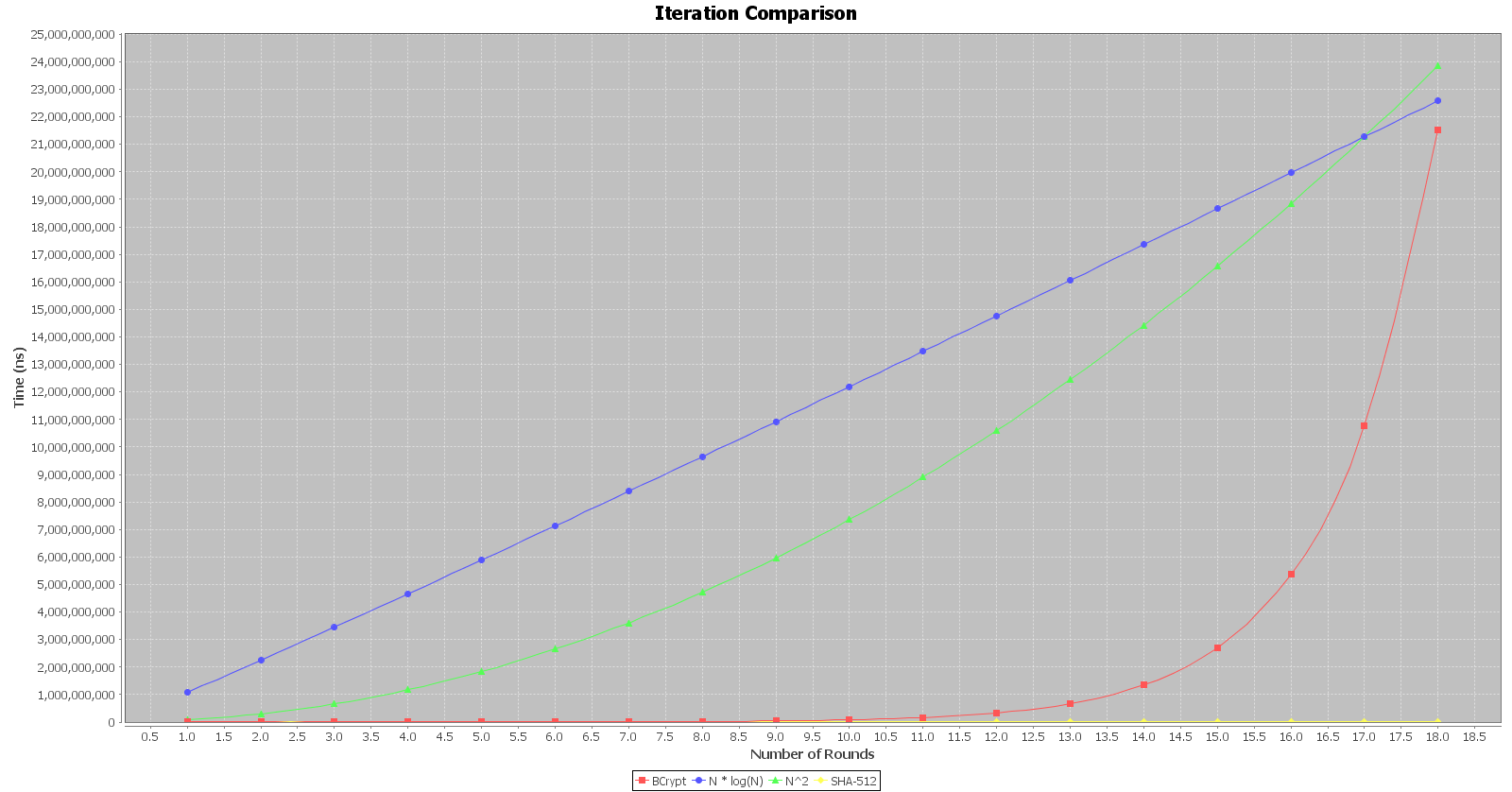
Not well. The SHA-512 looks like a straight line when compared to bcrypt. Furthermore, bcrypt stores the number of iterations in the hash, enabling the number of iterations to be modified with ease.